DAY 17. Character Sets

• Sets and Set Theory
• Implementation of Character Sets
• Creating a Character Set
• Performing Set Operations on Character Sets
• Testing Character Sets

Sets and Set Theory

1. Each member of the set is unique, there can never be more than one of the same set member.
2. The members of a set are unordered.
3. An element can either be a member to a set or not, there are no in-betweens.

{ 0, x, ö, 9, 12, A }
The set of the letters 'x', 'ö', 'A', and the integers '0', '9', '12'.

{ all positive small integers }
The set 1, 3, 5, 7, ...

{ x | x! <= 120 }
The set 1, 2, 6, 24, 120

If a set has no members, it is called the empty set and is denoted Æ, which must be at least just a little annoying to the Swedes.

Things to do to Your Sets

Complement

Union

Intersection

Difference

Subset

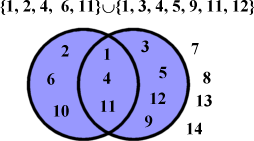
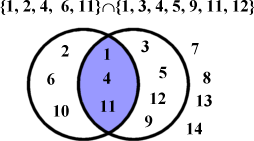
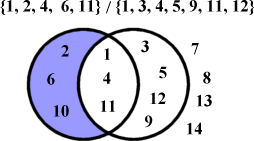
A proper subset is one that is dissimilar to its parent set. E.g. if you were a real tightwad and bought all your books paperbacked and second-hand, then for you the set of you paperback books would be a subset of all you books, but it would not be a proper subset.

Superset

Implementation of Character Sets

Bit seven of byte 0 corresponds to ASCII code 0. If this bit is set, the character set contains ASCII 0 as a member. The next bit over is for ASCII 1, and so on up to ASCII 127. Here is what a set corresponding to the string "Electromagnetic radiation" would look like:

                                     !"#$%&' ()*+, -./ 01234567 89:;<=>?
00000000 00000000 00000000 00000000 10000000 00000000 00000000 00000000
@ABCDEFG HIJKLMNO PQRSTUVW XYZ[\]^_ `abcdefg hijklmno pqrstuvw xyz{|}~
00000100 00000000 00000000 00000000 01011101 01001111 00101000 00000000

Creaing a Character Set

How about adding a character to a pre-existing character set? We can do that with a little bitmasking.
To set a bit we want a bitmask that, when ORed with the character set, sets the bit for the character. For that we need to know a) the byte and b) the bit in that byte. To get the byte, the charset is 16 bytes long and contains 128 elements. 128 ÷ 16 = 8, so divide the character's ASCII code by 8. Add the quotient to the base address and we have our byte. To get the bit, find the remainder of that division.
Now, create a bitmask by rotating the value %10000000 to the right by the bit number, and then OR it with the byte of the charset.

E.g. To our previous character set, we would like to add the letter 'U' (ASCII 85). Divide 85 by 8 to get 10, therefore we will be working with the eleventh byte of the charset. The remainder of 85 ÷ 8 is 5, so rotate %10000000 five times to the right to get %00000100, and OR it. The character set is now:

                                     !"#$%&' ()*+, -./ 01234567 89:;<=>?
00000000 00000000 00000000 00000000 10000000 00000000 00000000 00000000
@ABCDEFG HIJKLMNO PQRSTUVW XYZ[\]^_ `abcdefg hijklmno pqrstuvw xyz{|}~
00000100 00000000 00000100 00000000 01011101 01001111 00101000 00000000

    LD    C, A
    SRL   C
    SRL   C
    SRL   C
    LD    B, 0
    ADD   HL, BC
    AND   7
    LD    B, A
    LD    A, %10000000
    JR    Z, Insert
Shift:
    RRCA
    DJNZ  Shift
Insert:
    OR    (HL)
    LD    (HL), A

A character set for an entire string can be created by starting with the empty set and adding each character of the string in sequence.

It might be useful to remove a character from a character set. It follows the same principle for insertion, only use %01111111 as the initial bitmask, and use AND logic.

Performing Set Operations on Character Sets

; Union of the character set pointed to by HL and the one pointed to by DE
    LD    B, 16
Loop:
    LD    A, (DE)
    OR    (HL)
    LD    (HL), A
    DJNZ  Loop

The other set operations are likewise calculated using the appropriate boolean instructions: AND for intersection, AND CPL for difference.

Testing Character Sets

Most often, you will want to see if a specific character is in a character set. The way to do this is with an AND bitmask that is entirely made up of zeros save for the bit corresponding to the character to test for set membership. The mask clears all of the other seven bits, and if the character does indeed belong to the set, the Z will be reset (because, you know, it'll be a 1 ANDed with a 1).

Two character sets are equal if the all the bits are equal. You can check two sets for equality or inequality by performing a multiprecision comparison of the sets.

    LD    BC, 16
Loop:
    LD    A, (DE)
    CPI
    JR    NZ, Break
    INC   DE
    JP    PE, Loop
Break:

To test for a subset, you first have to find the set intersection. If the intersection is equal to the first set, then the second set is a subset of the first. If the set intersection is also not equal to the second set, then you have a proper subset on your hands. The implementation of the superset and proper superset test are identical.